Content Markup
(Excerpt from "The MathML Handbook" by Pavi Sandhu)
MathML content markup consists of about 150 elements and 12 attributes. The majority of content elements are empty elements that represent a specific operator, function, or relation. Examples of such elements are plus, power, log, and sin.
Content markup also contains three different token elements, cn, ci, and csymbol, which are used to encode numbers, identifiers, and user-defined symbols, respectively. Content token elements are the only content elements that can directly contain character data. All other content elements are either empty elements or can contain only other content elements.
The single most important content element is the apply element, which is used to apply operators or functions to expressions. The first argument of the apply element is typically an element that represents an operator or function. The remaining arguments represent one or more expressions to which the first argument is applied.
Content markup is based on the concept of prefix notation, a convention for writing mathematical expressions that is used in programming languages like LISP. In prefix notation, any expression is written as an operator followed by the objects it operates on, namely its operands. For example, to represent x + y in prefix notation, you would write something like + x y. Similarly, to represent x², you would write Power x 2. You can represent more complicated expressions in prefix notation by nesting and combining smaller subexpressions.
To get the content markup for an expressions, you first write the expression in prefix notation; then you replace each operator and operand by the corresponding content elements. Here is a simple example of content markup:
x²
<math>
<apply>
<power/>
<ci>x</ci>
<cn>2</cn>
</apply>
</math>
The markup consists of a single apply element, followed by three elements that each represent an argument of the apply element. The first element is the empty element power, which represents the function to be applied. The next two elements, ci and cn, represent the arguments to which the power function is applied. The ci element represents the base and the cn element the power.
Here is the content markup for the expression x + y:
x + y
<math>
<apply>
<plus/>
<ci>x</ci>
<ci>y</ci>
</apply>
</math>
The markup consists of a single apply element followed by a plus element (which represents the function to be applied) and two ci elements (which represent the arguments to which the plus function is applied).
Here is the content markup for a slightly more complicated expression:
(x + y)²
<math>
<apply>
<power/>
<apply>
<plus/>
<ci>x</ci>
<ci>y</ci>
</apply>
<cn>2</cn>
</apply>
</math>
This markup combines elements of both the previous examples. It uses two nested apply elements. The inner apply element is used to encode the sum x + y, and the outer apply element is used to raise the summed expression to the power of two.
Here is the content markup for a simple algebraic expression:
x² - 2x + 1
<math>
<apply>
<plus/>
<apply>
<minus/>
<apply>
<power/>
<ci>x</ci>
<cn>2</cn>
</apply>
<apply>
<times/>
<cn>2</cn>
<ci>x</ci>
</apply>
</apply>
<cn>1</cn>
</apply>
</math>
This example uses the apply, plus, and power elements that we saw in combination with the minus and times elements. The last two elements represent subtraction and multiplication, respectively.
The following example illustrates how to represent fractions and square roots using content markup:
![]()
<math>
<apply>
<divide/>
<apply>
<plus/>
<cn>1</cn>
<apply>
<root/>
<cn>5</cn>
</apply>
</apply>
<cn>2</cn>
</apply>
</math>
The square root is encoded using the root element. You can also use this element to represent radicals by specifying the degree of the radical as the second argument. As you can see, more complicated expressions are built up in a straightforward way by combining and nesting smaller subexpressions, as required.
Here is the content markup for a simple matrix:
![]()
<math>
<matrix>
<matrixrow>
<ci>a</ci>
<ci>b</ci>
</matrixrow>
<matrixrow >
<ci>c</ci>
<ci>d</ci>
</matrixrow >
</matrix>
</math>
Here is the content markup for an equation involving an integral:
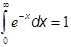
<math>
<apply>
<eq/>
<apply>
<int/>
<bvar>
<ci>x</ci>
</bvar>
<lowlimit>
<cn>0</cn>
</lowlimit>
<uplimit>
<infinity/>
</uplimit>
<apply>
<power/>
<exponentiale/>
<apply>
<minus/>
<ci>x</ci>
</apply>
</apply>
</apply>
<cn>1</cn>
</apply>
</math>
In the above example, the int element is used to represent an integral. The lowlimit, uplimit, and bvar elements are used to represent the upper limit, lower limit, and variable of integration, respectively. The constants ∞ and e are represented using the content elements infinity and exponentiale, respectively.
| << back | next >> |
| Tipp der data2type-Redaktion: Zum Thema MathML bieten wir auch folgende Schulungen zur Vertiefung und professionellen Fortbildung an: |
Copyright © CHARLES RIVER MEDIA, INC., Massachusetts (USA) 2003
Printing of the online version is permitted exclusively for private use. Otherwise this chapter from the book "The MathML Handbook" is subject to the same provisions as those applicable for the hardcover edition: The work including all its components is protected by copyright. All rights reserved, including reproduction, translation, microfilming as well as storage and processing in electronic systems.
CHARLES RIVER MEDIA, INC., 20 Downer Avenue, Suite 3, Hingham, Massachusetts 02043, United States of America







