Using cross-references
(Excerpt from "The MathML Handbook" by Pavi Sandhu)
By using a sufficient number of semantics elements, you can explicitly specify down to as small a level as desired the correspondence between content and presentation encodings of sub-expressions of the main expression. However, the limitation of this approach is that the markup quickly becomes very verbose, which leads to a large increase in the size of the document.
A more efficient way to specify fine-grained markup is to use the id and xref tags, which all MathML elements support. These tags provide a compact way to create cross-references between different parts of the expression tree. You can then use cross-references to associate content elements with the corresponding presentation elements, down to the level of the individual token elements that represent the leaves of the expression tree — namely, numbers, operators, and identifiers.
The id and xref attributes can be set to any arbitrary value, as long as that value is unique within the document. Any element with an id attribute then defines a target, which is referenced by all elements that have an xref attribute with the same value. The following markup uses cross-references to represent the same expression used in the last example:
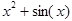
<semantics>
<mrow id="A">
<msup id="A.1">
<mi id="A.1.1">x</mi>
<mn id="A.1.2">2</mn>
</msup>
<mo id="A.2">+</mo>
<mrow id="A.3">
<mi id="A.3.1">sin</mi>
<mo id="A.3.2">⁡</mo>
<mo id="A.3.3">(</mo>
<mi id="A.3.4">x</mi>
<mo id="A.3.5">)</mo>
</mrow>
</mrow>
<annotation-xml encoding='MathML-Content'>
<apply xref="A">
<plus xref="A.2"/>
<apply xref="A.1">
<power/>
<ci xref="A.1.1">x</ci>
<cn xref="A.1.2">2</cn>
</apply>
<apply xref="A.3.2">
<sin xref="A.3.1"/>
<ci xref="A.3.4">x</ci>
</apply>
</apply>
</annotation-xml>
</semantics>
Notice that the content and presentation encodings of the entire expression, x2 + sin(x), are associated using id and xref attributes with the value A. Moving one level down the expression tree, the two encodings of the term x2 are identified using the id and xref pairs having the value A.1. Finally, the token elements in the content and presentation markup, describing the identifier x and the number 2 in the first term, are identified using the values A.1.1 and A.1.2.
| << back | next >> |
| Tipp der data2type-Redaktion: Zum Thema MathML bieten wir auch folgende Schulungen zur Vertiefung und professionellen Fortbildung an: |
Copyright © CHARLES RIVER MEDIA, INC., Massachusetts (USA) 2003
Printing of the online version is permitted exclusively for private use. Otherwise this chapter from the book "The MathML Handbook" is subject to the same provisions as those applicable for the hardcover edition: The work including all its components is protected by copyright. All rights reserved, including reproduction, translation, microfilming as well as storage and processing in electronic systems.
CHARLES RIVER MEDIA, INC., 20 Downer Avenue, Suite 3, Hingham, Massachusetts 02043, United States of America







