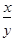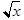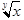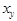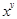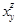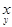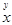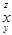Mathematica syntax

(Excerpt from "The MathML Handbook" by Pavi Sandhu)

There is a close correspondence between MathML and the syntax used internally by Mathematica to represent mathematical formulas. The Mathematica syntax is, in effect, a text-based markup language for representing mathematical formulas and capturing both their notation and meaning. Because it provides a flexible and powerful system for describing mathematics, Mathematica was an important influence in the design of MathML. There are many points of similarity between the structure of MathML and the syntax of Mathematica expressions. In this section, we briefly review some details of Mathematica syntax and see how it compares with MathML.

Like MathML, Mathematica makes a distinction between the semantic meaning of a mathematical formula and its visual structure. The semantic meaning of any formula is represented internally using what is called its full form. This is a symbolic expression built up from standard Mathematica function names. The full form of a formula is closely analogous to MathML content markup. The appearance of mathematical notation, on the other hand, is described using a series of box structures, which are analogous to MathML presentation markup. Mathematica can freely convert between full-form expressions and boxes, using the former for performing computations and the latter for displaying mathematics in a notebook.

FullForm and content MathML

The underlying logical structure of any mathematical formula, which determines its semantic interpretation, is called its full form. You can see the full form, of any expression expr by evaluating the command FullForm[expr]. For example, the following command shows the full form of the expression x² + y:

In[1]:= FullForm[x^2+y]
Out[2]//FullForm= Plus[Power[x, 2], y]

The //FullForm annotation is added to the Out label to indicate that the output is being displayed in FullForm.

The content markup representation for the same expression would be as follows:

You can see that the Mathematica full form of an expression and its content markup representation are very similar. Both use prefix functional notation to recursively build up complicated expressions out of smaller building blocks. The main difference is that in Mathematica, function application is indicated as 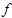[x], where 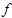is a specific Mathematica command such as Plus, Power, Sin, or Integrate. In content MathML, on the other hand, function application is indicated as <apply>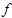x</apply>, where 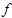is a content markup element that represents a specific operator or function, such as plus, power, sin, or int. Also, the atomic units of mathematical notation (numbers, operators, and identifiers) are all denoted by a separate element in MathML, while Mathematica does not make any distinction between these different types of objects, encoding them all as strings.

Boxes and presentation MathML

To describe the two-dimensional appearance of mathematical notation, Mathematica uses a series of box structures. There are different types of boxes for describing subscripts, superscripts, or fractions. Each of these box structures is in the form of a symbolic expression that can take one or more arguments. For example, the formula x² + y is represented in Mathematica by the following symbolic expression:

RowBox[{SuperscriptBox["x", "2"], "+", "y"}]

There is a close correspondence between the box structures used in Mathematica and the presentation elements of MathML. For example, the above expression would be represented in presentation markup as shown below:

You can see that the RowBox[...] and SuperscriptBox[...] constructs in Mathematica are equivalent to the <mrow>...</mrow> and <msup>...</msup> constructs in MathML. In each case, the child elements of the MathML presentation element are equivalent to the arguments of the Mathematica box expression. In the box expressions, as with full form, numbers, operators, and identifiers are all represented as strings.

A more complete listing of some Mathematica notational structures and their MathML counterparts is given in the following table. The different types of boxes can be nested and combined, as necessary, to represent more complicated expressions.

Table: Mathematica notational structures and their MathML counterparts.

You can see the underlying structure of any mathematical formula in a notebook by selecting the expression and choosing Format → Show Expression from the menu. The following figure shows a formula in a notebook and the figure after this shows the underlying expression for the formula.

Figure: A mathematical formula in a notebook.

Figure: The underlying box structure of the formula shown in the figure above as displayed by using the Format → Show Expression command.

Display forms

Mathematica supports several different forms for the display of mathematics. A given formula can have several different textual representations, each corresponding to a different way of displaying the expression in a notebook. Some of the important display forms are:

• InputForm: is a linear text-based form that can be typed directly using only the characters on a standard keyboard.
• TraditionalForm: can display special characters and two-dimensional positioning to closely approximate traditional mathematical notation. It is not well-suited for computation since its mathematical meaning can be ambiguous.
• StandardForm: is a compromise between InputForm and TraditionalForm. It can display special characters and two-dimensional layout while still preserving an unambiguous mathematical meaning. By default, input and output in Mathematica notebooks are displayed in StandardForm.
• MathMLForm: displays the MathML markup for a mathematical expression. The markup is indented and formatted to reveal the hierarchical structure of the MathML expression.

Several other display forms (such as TeXForm and CForm) use the syntax of TeX and the C programming language, respectively. Forms that display expressions as a linear sequence of characters, such as FullForm and InputForm, are represented in Mathematica as simple strings. Forms that display two-dimensional notation, such as StandardForm and TraditionalForm, are represented using the box structures described earlier.

To see an expression, expr, displayed in a particular form, you can type and evaluate the command form[expr]. Here are some examples of the same expression displayed in several different forms.

In StandardForm, the text is in a monospaced font, and square brackets are used for function application:

In[1]:= StandardForm[x^2+1/Log[x]]

Out[1]//StandardForm=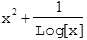

In TraditionalForm, variables are shown in italics, and parentheses are used for function application:

In[2]:= TraditionalForm[x^2+1/Log[x]]

Out[2]//TraditionalForm=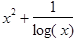

InputForm does not support two-dimensional display, so information about fractions and powers, for example, is shown in a linear syntax:

In[3]:= InputForm[x^2+1/Log[x]]

Out[3]//InputForm= x^2 + Log[x]^(-1)

You can also convert a formula from one display form to another by selecting the formula and choosing the appropriate form in the Cell → Convert To menu (see the following figure)

Figure: The Cell → Convert To menu for changing between different display formats.

The following figure shows a notebook that contains an integral. Both the input and output are in StandardForm by default. ArcSin and Zeta are built-in Mathematica commands that represent the inverse sine and Riemann zeta functions, respectively.

Figure: A mathematical formula, displayed in StandardForm, in a notebook.

The next figure shows the same input and output cells from the last figure after they are converted to TraditionalForm using the Cell → Convert To → TraditionalForm menu. Notice that the ArcSin and Zeta functions are automatically displayed in the traditional notation for these functions.

Figure: The same formula as in the last figure after conversion to TraditionalForm.

There are also several functions for converting between full form expressions and the various display forms (based on strings and boxes):

• ToString[expr, form]: creates a string that represents the specified textual form of expr.
• ToBoxes[expr, form]: creates boxes that represent the specified textual form of expr.
• ToExpression[input, form]: creates an expression by interpreting a string or boxes as input in the specified textual form.

The aim of this section is to provide an overview of the syntax used in Mathematica for representing the meaning and appearance of mathematical notation. If you want more details about the different types of expressions and display forms, you should consult the Mathematica documentation.