Presentation markup
(Excerpt from "The MathML Handbook" by Pavi Sandhu)
MathML presentation markup consists of about 30 elements and 50 attributes. The most important presentation elements are the so-called token elements — mo, mn, and mi — which are used to represent operators (such as + or –), numbers (such as 3.14 or –27), and identifiers (that is, variables like x or y), respectively.
Token elements are the only presentation elements that can directly contain character data. All other elements can only contain other MathML elements. The reason for using separate elements to represent operators, numbers, and identifiers is so that each type of item can be rendered according to its own typesetting conventions. For example, operators have extra spacing around them, numbers are usually shown in an upright font, and identifiers are typically italicized.
This simple example of presentation markup encodes the expression x + y:
x + y
The outermost element of the expression is a math element, as required for any piece of MathML markup. The rest of the markup consists of two mi elements for representing the identifiers x and y and an mo element representing the operator +. These are all enclosed in an mrow element, which causes its child elements to be displayed in a horizontal row.
Here is the presentation markup for a slightly more complicated expression:
(x + y)²
The first element in the markup after the math element is msup, which reflects the fact that the encoded expression consists of a base with a superscript. The msup element has two arguments, which represent the base expression and the superscript, respectively. That is, it has the syntax: <msup>base index</msup>. The base and index terms can either be token elements or more complicated expressions consisting of other MathML elements.
In the above example, the base consists of a single mrow element that is used to encode the expression x + y. The superscript (that is, the second argument of the msup element) is the number 2 enclosed in an mn element to indicate that it is a number.
This example indicates some general principles that you can use to determine the presentation markup for any mathematical expression. Each expression is decomposed into its constituent subexpressions, and the process is continued recursively until one reaches the fundamental or atomic units of the expression, namely numbers, operators, or identifiers. The atomic units are represented by the appropriate token elements. All other subexpressions are then represented by the corresponding MathML presentation elements, so that the recursive structure of the MathML tree exactly duplicates the recursive structure of the original expression.
Here is the presentation markup for a simple quadratic polynomial:
x² - 2x + 1
This example uses the mrow and msup elements introduced in the previous example, along with the token elements mi, mn, and mo. The additional feature here is the use of the entity reference ⁢ to indicate that the 2 and the x are being multiplied together. The use of this entity reference is not required, since the visual display of the equation is unaffected if the <mo>⁢</mo> element is omitted altogether.
However, if you explicitly include the entity reference, the markup gives additional information about the meaning of the equation. This information is useful, for example, when you are evaluating the markup in a computer algebra system or converting it to an audio rendering. Hence, the use of such entities is strongly encouraged in presentation MathML. Note that for applications in which interpreting the meaning of an equation is important, the use of content MathML would be preferable.
The following example illustrates how you can use presentation markup to represent fractions and square roots:
![]()
The mfrac and msqrt elements are used to represent fractions and square roots, respectively. The mfrac element has the syntax: <mfrac>num denom</mfrac>, where the first argument is the numerator and the second argument is the denominator.
Here is the presentation markup for the solution of a general quadratic equation:
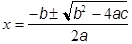
<math>
<mrow>
<mi>x</mi>
<mo>=</mo>
<mfrac>
<mrow>
<mo>-</mo>
<mi>b</mi>
<mo>±</mo>
<msqrt>
<mrow>
<msup>
<mi>b</mi>
<mn>2</mn>
</msup>
<mo>-</mo>
<mrow>
<mn>4</mn>
<mo>⁢</mo>
<mi>a</mi>
<mo>⁢</mo>
<mi>c</mi>
</mrow>
</mrow>
</msqrt>
</mrow>
<mrow>
<mn>2</mn>
<mo>⁢</mo>
<mi>a</mi>
</mrow>
</mfrac>
</mrow>
</math>
This example uses several of the presentation elements introduced so far: mrow, msqrt, msup, and mfrac. It differs from the previous example only in the complexity of the nesting: the markup has a larger number of elements that reflect the complexity of the layout tree from which the expression is composed. Note the use of the entity reference ⁢ to explicitly indicate multiplication. The example also uses the entity reference ± to represent the ![]() symbol.
symbol.
Here is the presentation markup for a simple matrix:
![]()
The outermost element of the matrix is an mtable element, which is used to represent any type of table or array. Each row of the table is enclosed in an mtr element, and each entry or cell in a row is enclosed in an mtd element. The parentheses surrounding the matrix are indicated explicitly using mo elements.
Here is the presentation markup for an equation involving an integral:
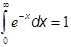
The only new element introduced in this example is msubsup, which has the syntax: <msubsup>base subscript superscript</msup>. This element is used to position a subscript and superscript symmetrically about a base expression. Note the use of the named entity references ∫, ⅇ, and ⅆ to represent the integral, exponential, and differential d symbols, respectively. As with the use of ⁢, the use of these named character references provides useful information about the meaning of the expression.
| << back | next >> |
Copyright © CHARLES RIVER MEDIA, INC., Massachusetts (USA) 2003
Printing of the online version is permitted exclusively for private use. Otherwise this chapter from the book "The MathML Handbook" is subject to the same provisions as those applicable for the hardcover edition: The work including all its components is protected by copyright. All rights reserved, including reproduction, translation, microfilming as well as storage and processing in electronic systems.
CHARLES RIVER MEDIA, INC., 20 Downer Avenue, Suite 3, Hingham, Massachusetts 02043, United States of America

