Semantic mapping elements
(Excerpt from "The MathML Handbook" by Pavi Sandhu)
Content markup describes the logical meaning of mathematical expressions. However, there are many situations in which it is useful to supplement the content markup with additional information. For example, you might want to include the presentation markup for an expression along with the content markup to specify that the expression be rendered in a special form that is different from the default rendering that would be used if the content markup alone were specified by itself.
Alternatively, you might want to include the representation of a mathematical expression in another computer language (such as TeX, C, or Mathematica) for use by particular applications that recognize those languages. This type of additional information is called a semantic mapping. MathML provides three content elements for specifying semantic mappings: semantics, annotation, and annotation-xml.
The semantics element is used as a container element for the MathML expression and all its semantic mappings. This element takes one or more child elements. The first element is the MathML expression for which semantic mappings are to be specified, and the subsequent arguments are the semantic mappings themselves. Each semantic mapping is enclosed in an annotation or annotation-xml element.
The semantics element accepts a definitionURL attribute you can use to specify a URL that contains the semantic mapping for the expression. The presence of the annotation and annotation-xml elements is optional since you can specify the semantic mapping completely by using only the definitionURL attribute.
The annotation element can contain any arbitrary character data. The format of the data is indicated using the value of the encoding attribute. For example, you could include the Mathematica command that corresponds to a given MathML expression by specifying encoding="mathematica" or you could give the TeX equivalent by specifying encoding="TeX".
The annotation-xml element also specifies a semantic mapping but with the additional constraint that its content must be a well-formed XML expression. The format of the mapping is specified using the encoding attribute. Typical values of this attribute are Presentation-MathML (for presentation markup), Content-MathML (for content markup), or OpenMath. The OpenMath consortium is a regulatory body that has developed a platform-independent and vendor-neutral standard for specifying the semantic meaning of mathematical expressions. The OpenMath specification of any mathematical expression is written in XML; hence, OpenMath statements are suitable for inclusion in an annotation-xml element.
The following example shows a content MathML expression with three semantic mappings specified:
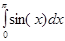
<semantics>
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<lowlimit><cn>0</cn></lowlimit>
<uplimit><pi/></uplimit>
<apply><sin/><ci>x</ci></apply>
</apply>
<annotation-xml encoding="MathML-Presentation">
<mrow>
<munderover>
<mo>∫</mo><mn>0</mn><mi>π</mi>
</munderover>
<mrow>
<mrow>
<mi>sin</mi><mo>⁡</mo>
<mo>(</mo><mi>x</mi><mo>)</mo>
</mrow>
<mo>⁢</mo>
<mrow>
<mo>ⅆ</mo><mi>x</mi>
</mrow>
</mrow>
</mrow>
</annotation-xml>
<annotation encoding="TeX">$$\int_0^\pi {\sin(x)dx}$$</annotation>
<annotation encoding="Mathematica">Integrate[Sin[x],{x,0,Pi}]</annotation>
</semantics>
Above, the presentation markup encodings are included in an annotation-xml element, while the TeX and Mathematica encodings are each included in an annotation element. The original expression, along with all three semantic mappings, is enclosed in a semantics element.
| << back | next >> |
Copyright © CHARLES RIVER MEDIA, INC., Massachusetts (USA) 2003
Printing of the online version is permitted exclusively for private use. Otherwise this chapter from the book "The MathML Handbook" is subject to the same provisions as those applicable for the hardcover edition: The work including all its components is protected by copyright. All rights reserved, including reproduction, translation, microfilming as well as storage and processing in electronic systems.
CHARLES RIVER MEDIA, INC., 20 Downer Avenue, Suite 3, Hingham, Massachusetts 02043, United States of America

