Token elements
(Excerpt from "The MathML Handbook" by Pavi Sandhu)
Content markup contains three token elements: cn, ci, and csymbol. The cn and ci elements are analogous to the mn and mi elements in presentation markup; that is, they are used to represent numbers and identifiers, respectively. The csymbol element is used to associate a specific mathematical meaning with a particular symbol. Token elements have a special status since they are the only content elements that can directly contain character data. Token elements can also contain arbitrary presentation markup, which allows you to have greater control over how they are rendered.
Numbers
The cn element is used to represent numbers. Its content consists of an optional '+' or '-' sign followed by a string of digits, possibly containing a decimal point. Alternatively, the cn element can contain one of the named entity references that represent a numerical constant, such as π or ⅇ. By default, the contents of the cn element are interpreted as a signed real number in base 10. However, you can specify a different type of number or a different base, using the type and base attributes.
The type attribute of the cn element describes the type of number encoded. It can take the values real, integer, rational, complex-polar, complex-cartesian, e-notation, and constant. The empty element sep is used to separate different parts of a number (such as the numerator and denominator of a fraction or the real and imaginary parts of a complex number). For example, a fraction is represented as shown here:
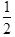
<cn type="rational">1<sep/>2</cn>A complex number is represented as shown here:
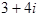
<cn type="complex-cartesian">3<sep/>4</cn>The base attribute of the cn element specifies the base of the number being encoded. It can be any number between 2 and 36. For example, a hexadecimal number would be represented as shown here:
EF216
<cn type="integer" base="16">EF2</cn>The following table gives a few examples of some other types of numbers that can be represented using the cn element.
Table: Types of numbers represented by the cn element.
| Number | Content markup |
|---|---|
765.43 | <cn type="real">765.43</cn> |
2002 | <cn type="integer">2002</cn> |
Polar(5, 3.14) | <cn type="complex-polar">5<sep/>3.14</cn> |
π | <cn type="constant">π</cn> |
In addition to type and base, the cn element takes the definitionURL and encoding attributes, which can be used to modify its default semantics, as explained under Introduction.
Identifiers
The ci element is used to represent identifiers such as the names of variables or functions. Each ci element represents a single mathematical object. However, you can make its appearance as complex as you want by including any type of presentation markup inside it. For example, the following markup can be used to represent the second component of a vector x:
x2
<ci>
<msub>
<mi>x</mi>
<mn>2</mn>
</msub>
</ci>
You can indicate the type of object represented by using the type attribute, which can take values real, integer, rational, complex-polar, complex-cartesian, and constant. In addition, you can set the type attribute to the names of container elements in content markup, such as vector, matrix, set, and fn. An application can use the information in the type attribute to determine how the content should be rendered. For example, the following markup might be rendered in a bold font to indicate that it represents a vector:
<ci type="vector">A</ci>Symbols
The csymbol element is used to associate a specific mathematical meaning with a particular symbol. It can contain any presentation markup inside it, so you can specify the rendering of the symbol precisely.
This element is provided as an extension mechanism. In effect, it enables you to create a new symbol with a specific user-defined meaning. You can then use that symbol to represent any operator, function, or constant that is not described by any of the existing content elements. The meaning associated with the symbol is specified using the definitionURL and encoding attributes, as explained under Introduction.
For example, the following markup associates the symbol 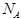 with the value of Avogadro's constant, used in chemistry:
with the value of Avogadro's constant, used in chemistry:
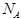
<csymbol encoding="text" definitionURL="www.example.org/universalconstants/Avogadro.htm" >
<msub>
<mi>N</mi>
<mi>A</mi>
</msub>
</csymbol>
The following example defines the notational unit 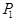 to mean the first Legendre polynomial function:
to mean the first Legendre polynomial function:
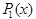
<apply>
<csymbol encoding="OpenMath" definitionURL="http://www.openmath.org/cd/LegendrePolynomial.ocd">
<msub>
<mi>P</mi>
<mn>1</mn>
</msub>
</csymbol>
<ci>x</ci>
</apply>
Here, the rendering of the symbol is specified using presentation markup and its meaning is specified in terms of the OpenMath convention, using the attributes of the csymbol element. You can then use this element as the first argument of an apply function.
| << back | next >> |
Copyright © CHARLES RIVER MEDIA, INC., Massachusetts (USA) 2003
Printing of the online version is permitted exclusively for private use. Otherwise this chapter from the book "The MathML Handbook" is subject to the same provisions as those applicable for the hardcover edition: The work including all its components is protected by copyright. All rights reserved, including reproduction, translation, microfilming as well as storage and processing in electronic systems.
CHARLES RIVER MEDIA, INC., 20 Downer Avenue, Suite 3, Hingham, Massachusetts 02043, United States of America

