XML technologies / MathML / Content markup / Operators and functions / Theory of sets

Theory of sets

(Excerpt from "The MathML Handbook" by Pavi Sandhu)

We have already seen the use of the constructor elements set and list to represent sets and lists. There are several content elements that represent various operators and functions used in the theory of sets.

The elements union and intersect are used to represent the union and intersection of two sets, as seen in the following example:

$Theory of sets: equation 1$

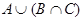
<apply>
  <union/>
  <ci type="set">A</ci>
  <apply>
    <intersect/>
    <ci type="set">B</ci>
    <ci type="set">C</ci>
  </apply>
</apply>

The elements in, notin, subset, prsubset, notsubset, notprsubset, and setdiff are used for representing various types of relationships between sets, as seen in the following examples:

$Theory of sets: equation 2$

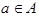
<apply>
  <in/>
  <ci>a</ci>
  <ci type="set">A</ci>
</apply>

$Theory of sets: equation 3$

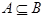
<apply>
  <subset/>
  <ci type="set">A</ci>
  <ci type="set">B</ci>
</apply>

The card element represents the cardinality of a set; that is, the number of elements it contains. Here is an example that uses this element:

| Z | 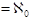$Theory of sets: equation 4$

<apply>
  <eq/>
  <apply>
    <card/>
    <integers/>
  </apply>
  <cn><msub><mn>&aleph;</mn><mn>0</mn></msub></cn>
  </apply>
</apply>

The setdiff element represents the difference of two sets. The cartesianproduct element represents the Cartesian product of two sets; that is, the set of all pairs (a, b) with 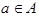and 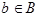. Using the elements described in this subsection, you can represent most mathematical statements encountered in the elementary theory of sets.

<< back

next >>

Copyright © CHARLES RIVER MEDIA, INC., Massachusetts (USA) 2003
Printing of the online version is permitted exclusively for private use. Otherwise this chapter from the book "The MathML Handbook" is subject to the same provisions as those applicable for the hardcover edition: The work including all its components is protected by copyright. All rights reserved, including reproduction, translation, microfilming as well as storage and processing in electronic systems.

CHARLES RIVER MEDIA, INC., 20 Downer Avenue, Suite 3, Hingham, Massachusetts 02043, United States of America