Introduction
(Excerpt from "The MathML Handbook" by Pavi Sandhu)
Some simple examples of content markup were discussed under Presentation and content. We saw there that content markup consists of approximately 150 elements and 12 attributes that are used to encode the logical meaning of mathematical expressions. Most content elements can be broadly divided into the following categories:
- Token elements
- Constructor elements
- Operators and functions
- Qualifier elements
- Constants and symbols
- Semantic mapping elements
Token elements are the only content elements that can directly contain character data. All other elements can contain only other elements. There are three token elements: cn, ci, and csymbol. These are used to represent numbers, identifiers, and user-defined symbols, respectively.
Constructor elements are used to construct expressions by combining token elements and elements that represent operators and functions. The most important constructor element is apply, which represents the operation of applying a function or operator to one or more arguments. By recursively nesting constructor elements, you can build up the content markup to represent an expression of any complexity. Token elements and constructor elements are collectively called container elements because they act as containers for mathematical objects.
The majority of content elements are empty elements that directly represent common operators and functions. Some elements that correspond to most operators and functions are encountered at the level of high school and college mathematics. For example, the plus, sin, and int elements represent addition, the trigonometric sine function, and integration, respectively.
Some content elements provide additional information needed to fully specify the meaning of other elements. For example, the uplimit, lowlimit, and bvar elements are used to specify the upper limit, lower limit, and variable of integration of a definite integral that is represented using the int element. These elements are called qualifier elements since they qualify the meaning of other elements.
A small number of content elements are used to directly represent specific constants and symbols that are important in mathematics. For example, the elements pi, exponentiale, imaginaryi, and infinity are used to represent the constants e, i, and ∞, respectively.
Semantic mapping elements are used to provide additional information, such as comments and annotations, about a given piece of content markup. For example, you can use the annotation element to give the encoding of a given MathML expression in another format such as TeX or Mathematica.
The following table lists all MathML content elements, organized into categories according to the type of element.
Table: Content elements.
| Category | Elements |
|---|---|
Token elements | ci, cn, csymbol |
Basic content elements | apply, lambda, declare, reln, fn, set, list, vector, matrix, matrixrow, interval, piecewise, piece, otherwise, domain, codomain, image, inverse, ident |
Arithmetic, algebra, and logic | plus, minus, times, divide, power, root, quotient, rem, exp, factorial, max, min, gcd, abs, conjugate, arg, real, imaginary, lcm, floor, ceiling, and, or, xor, not, implies, forall, exists |
Relations | eq, neq, gt, lt, geq, leq, equivalent, approx, factorof, tendsto, in, notin, subset, prsubset, notsubset, notprsubset |
Elementary functions | exp, ln, log, sin, cos, tan, sec, cosec, cot, sinh, cosh, tanh, sech, cosech, coth, arcsin, arccos, arctan, arcsec, arccosec, arccot, arcsinh, arccosh, arctanh, arcsech, arccosech, arccoth |
Theory of sets | set, list, union, intersect, setdiff, card, cartesianproduct |
Sequences and series | sum, product, limit |
Linear algebra | determinant, transpose, selector, vectorproduct, scalarproduct, outerproduct |
Calculus | int, diff, partialdiff, grad, divergence, curl, laplacian |
Statistics | mean, median, mode, var, sdev |
Qualifier elements | bvar, lowlimit, uplimit, degree, logbase, domainofapplication, momentabout |
Constants and symbols | pi, exponentiale, eulergamma, infinity, imaginaryi, true, false, emptyset, notanumber, integers, reals, rationals, complexes, primes, naturalnumbers |
Semantic mapping elements | semantics, annotation, annotation-xml |
Note:
For the sake of brevity, the math element is omitted from all examples in this chapter. However, this element is implied by the context; that is, you should think of each instance of MathML markup as being enclosed in an outer math element.
Modifying the default semantics
Each content element has a default semantic meaning. However, you can modify the meaning of any of these elements using the following two attributes, which most content elements accept:
- definitionURL: specifies a URL that contains information on the semantics of the symbol.
- encoding: specifies the form in which the semantic information is encoded.
For example, the content element times by default represents the operation of multiplying two numbers. However, you can modify its semantics so that it refers to the cross product of two vectors, as in the following example:
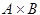
<apply>
<times encoding="text" definitionURL="http://www.example.org/vectorcrossproduct.html" />
<ci type="vector"> A </ci>
<ci type="vector"> B </ci>
</apply>
Here, the URL specified as the value of definitionURL must contain a definition of the vector product encoded as plain text. Note that the type attribute of the ci element is used to specify that the identifiers A and B represent vectors.
| << back | next >> |
Copyright © CHARLES RIVER MEDIA, INC., Massachusetts (USA) 2003
Printing of the online version is permitted exclusively for private use. Otherwise this chapter from the book "The MathML Handbook" is subject to the same provisions as those applicable for the hardcover edition: The work including all its components is protected by copyright. All rights reserved, including reproduction, translation, microfilming as well as storage and processing in electronic systems.
CHARLES RIVER MEDIA, INC., 20 Downer Avenue, Suite 3, Hingham, Massachusetts 02043, United States of America

