Sets and lists
(Excerpt from "The MathML Handbook" by Pavi Sandhu)
Sets and lists are represented using the set and list elements, respectively. Sets and lists are both used to represent a collection of elements that can be numbers, identifiers, or expressions. However, lists differ from sets in two important respects:
- In a list, the order of elements is significant. In contrast, two sets with the same elements are equivalent, regardless of the order in which the elements are written.
- In a list, each element can occur only once, whereas a set can contain repeated elements. The set element accepts the type attribute, which can take values normal or multiset, depending on whether repeated elements are allowed or not.
You can specify the elements of a set either by explicitly listing the elements or by using the bvar and condition elements to define a condition that elements of the set must satisfy. Here is an example of a set in which the elements are listed explicitly:
{0, 1, 2, 3}
<set>
<cn>0</cn>
<cn>1</cn>
<cn>2</cn>
<cn>3</cn>
</set>
Here is an example of the same set defined using a condition:
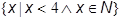
<set>
<bvar><ci>x</ci></bvar>
<condition>
<apply>
<and/>
<apply>
<lt/>
<ci>x</ci>
<cn>4</cn>
</apply>
<apply>
<in/>
<ci>x</ci>
<naturalnumbers/>
</apply>
</apply>
</condition>
<ci>x</ci>
</set>
As with sets, you can describe lists either by explicitly listing their elements or by using a condition. Here is an example of a list in which the elements are listed explicitly:
[0, 1, 2, 3]
<list>
<cn>0</cn>
<cn>1</cn>
<cn>2</cn>
<cn>3</cn>
</list>
Here is an example of the same list defined using a condition:
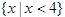
<list order="numeric">
<bvar><ci> x </ci></bvar>
<condition>
<apply>
<lt/>
<ci>x</ci>
<cn>5</cn>
</apply>
</condition>
<ci>x</ci>
</list>
You specify the ordering of the list elements by using the order attribute. This can take two values: numeric (which orders the elements in increasing numeric order) and lexicographic (which corresponds to an alphabetic ordering).
| << back | next >> |
Copyright © CHARLES RIVER MEDIA, INC., Massachusetts (USA) 2003
Printing of the online version is permitted exclusively for private use. Otherwise this chapter from the book "The MathML Handbook" is subject to the same provisions as those applicable for the hardcover edition: The work including all its components is protected by copyright. All rights reserved, including reproduction, translation, microfilming as well as storage and processing in electronic systems.
CHARLES RIVER MEDIA, INC., 20 Downer Avenue, Suite 3, Hingham, Massachusetts 02043, United States of America

